BOJ 4195 - python

4195 - 친구네트워크

• 문제유형 : 해시, 집합, 그래프
• 집합을 보다 효과적으로 표현할 줄 알아야 풀 수 있는 문제

문제풀이

• 문제가 요구하는 바는 정확하게 이해했음
• 집합을 효과적으로 사용하라고 해서 집합과 리스트를 연관지어서 생각해봤다.

  F = [{Fred,Berney},{Betty,Berney},{Betty,Wilma}]
  합집햡을 구하는 방법을 사용 
  temp = F[0] + F[1]
  F[0] = temp
  F[1] = temp
  F[0] = {Fred,Berney}, F[1]={Betty,Berney} -> F[0],F[1] = {Fred,Berney,Betty}
  

• 이렇게 temp라는 변수를 사용하여 합집합을 만들어서 해당 리스트요소를 변경하는 방식으로 생각했다.
• 한계 1 : 친구네트워크를 구성하는데에 있어서 앞의 리스트 요소와 중복되는 원소가 있는지여부 즉, 교집합이 존재하냐여부를 어떻게 구현할 지 명확하게 생각해내지 못했다.
• 한계 2 : for문을 너무 많이 썼다. -> 시간복잡도가 너무 큰 알고리즘(비효율적)
• 결국 끝까지 못풀었다.
• 친구를 하나의 node로 생각해야하는 것도 알겠는데, 구현을 못하겠다.

문제 풀이 핵심 아이디어

1. 해시를 활용한 union-find 알고리즘을 이용해 문제를 풀 수 있다.
   • union-find = 합집합 찾기
2. python에서는 dictionary자료형을 해시처럼 사용할 수 있다.

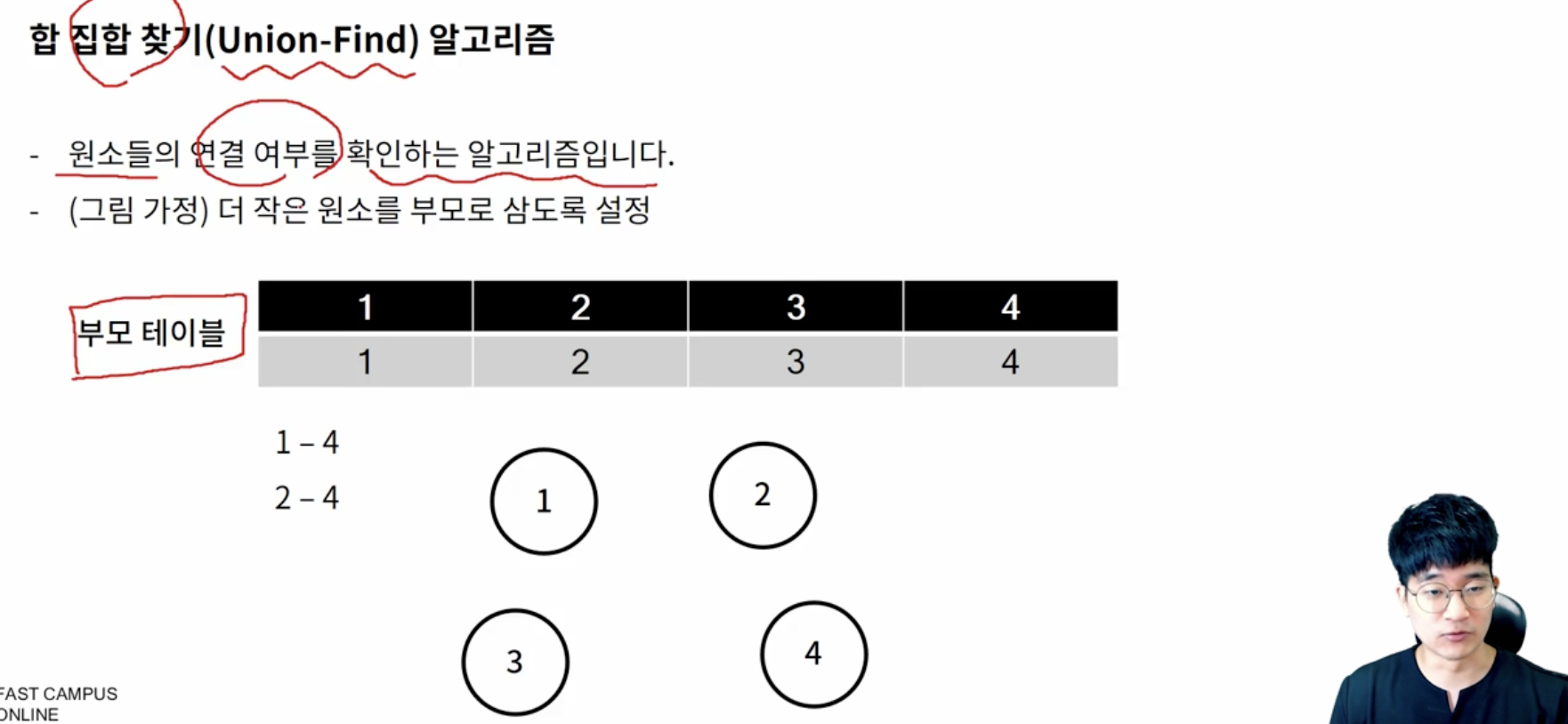
Union-Find 알고리즘

• 합집합 찾기 알고리즘 -> 원소들의 연결여부를 확인하는 알고리즘, 더 작은 원소를 부모로 삼도록 설정
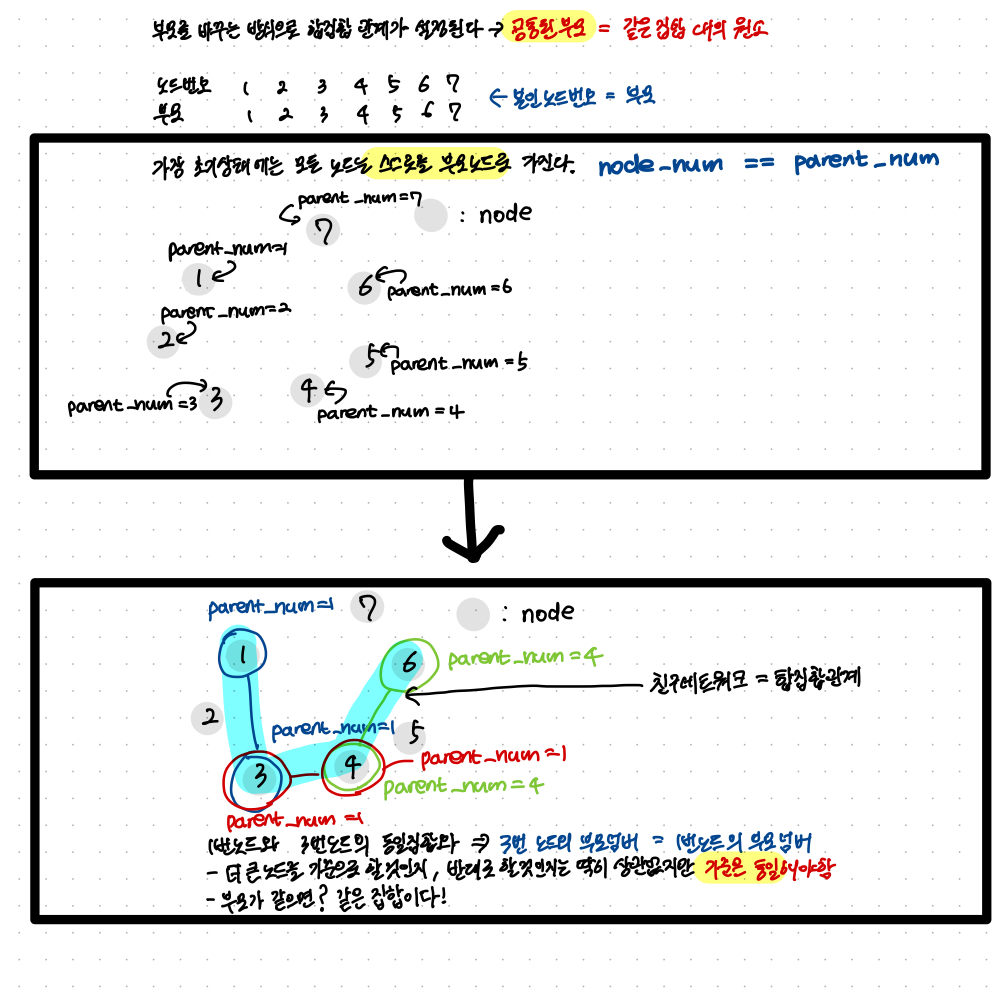
• • 가장 초기 상태 : 본인 만을 각각의 네트워크로 가진다.
• 부모테이블에서 parent_num이 1,2,3으로 3개이다 = 집합의 개수가 3개(노드의 개수와 관계 없음)
• 연결되어 있는 관계를 통해서 합집합을 구하는 것이 이 알고리즘의 핵심
• 예시 : 노드가 총 4개(node_num = 1,2,3,4)가 있다고 전제하자. 1번 노드와 4번 노드, 그리고 2번 노드와 4번 노드를 각각 연결하려고 한다. 직관적으로는 1-4, 2-4로 연결된다고 이해되지만, 사실상 재귀적으로 2번 노드와 4번 노드 모두 node_num이 가장 작은 1번 노드와 연결되어서 네트워크를 형성하고 있는 중이다. 왜냐하면 더 작은 원소를 부모로 삼기 때문이다.

def find(x) :
  if x==parent[x]:
      return x
  else:
     p = find(parent[x])//부모노드넘버 찾기
     parent[x] = p
     return parent[x]
     

• 출처 : [알고리즘] union-find 알고리즘
• Union : 2개 원소로 이루어진 집합을 하나의 집합으로 합치기
• find : 특정 원소가 속한 집합이 뭔지 알려주는 연산
  • 서로소 집합 자료구조는 union + find 연산으로 구성되므로 union-find 자료구조라고 불리기도 함
• union 연산 확인 => 서로 연결된 두 노드를 확인
  1. A의 루트 노드 A’과 B의 루트 노드 B’를 찾기 (find)
  2. A’를 B’의 부모 노드로 설정 (A’ < B’)
  3. 모든 union 연산을 처리할 때까지 1 반복